甲数是230,比乙数的2倍还多50,乙数是多少？如何用更容易理解的方法讲给差生？

这道题我已经进行了简化描述，原题是这样的：

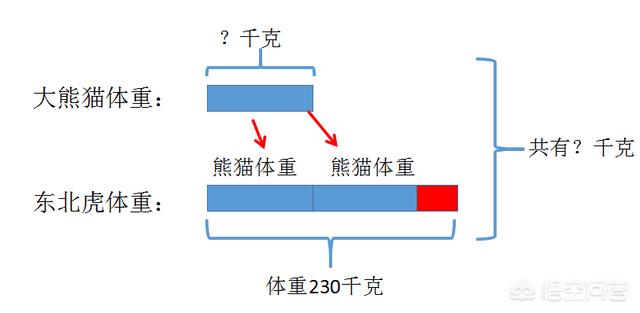
一头东北虎的体重大约是230千克，比一只大熊猫体重的2倍多50千克。一只大熊猫的体重大约是多少千克？

如图所示，原题的描述，几乎相当部分中、基础差的读完都可能是蒙的，再让他们理清有哪些量，量与量之间有什么关系，等量关系式真的是不可能完成的任务，这个从我收上来的作业中就会发现很多这样的问题，因为不懂题意，理不清两个数量之间的什么样的关系，基本就是见“多”就用加法。（因为是三年级，不涉及到方程）

数学题解题基本思路：

看了很多回答，有一个关键点我们都是统一的，就是找好标准量和比较量，同时一定要让学生确定出哪个量大，哪个量小，这一点真的很关键，毕竟仍然有部孩子真的是撞大运，看到有“多”字或者“少”字直接就用加法或者减法，这个时候就只能通过所计算出来的结果根据判断大小来验证自己的正确与否。如果答案和自己判的大小量是相反的，那直接能“多”或者“少”来确实加减就是错误的，这样纠正起来也就容易了，当然不管怎么说，这就是买500万中彩票的问题了，但也能够提高一点运气和正确率。所以如果简单的讲，不管你用加或者减，你一定要判断出到底哪个量大或者哪个量小，从理论上来说帮助你判断你答案的合理性。

对于这道题，我和大部分老师的思路是一样的，是结合画线段图来帮助理解：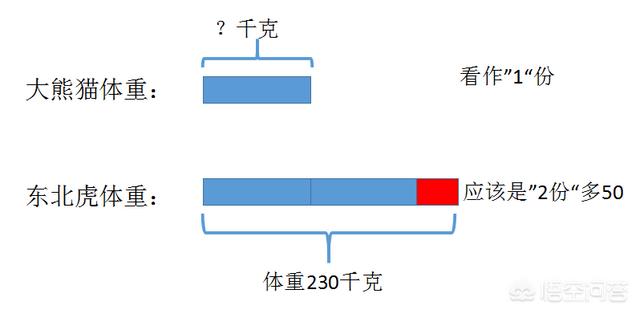

画图的原则：

1、先画标准量，也就是我们一般判断的是较小的那个量。

2、可以用线段或者像上面的用长方形小块来表示，可能更直观一些。

3、画中必须标出已经条件和所求的问题。

这道题的关键理解：

就是已知东北虎体重230千克如何表示，直接说就用一样什么样的关系式把东北虎体重表示出来。

注意箭头处，东北虎的体重可以这样来描述：两个大熊猫的体重（2倍或者2份）还需要加上红色部分（多余的50千克）才是东北虎的体重，即：

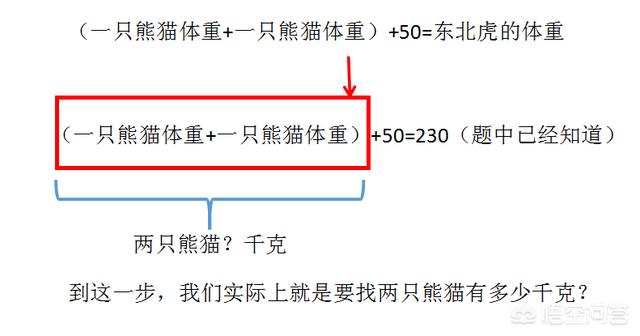
正确情况下到了这一步，应该能够算出两只熊猫的体重：230-50=180(千克）。

所以一只熊猫的体重就应该为：90+90=180，即每只熊猫为90千克，基础差的只能这样引导，两个一样的数加起来等于180，想想这个数是多少？基础好的就会用算式：180除以2=90千克。

再次，从份数来理解的话，可能基础比较好的，就可以直接从图上问他们，东北虎中的两份对应的体重是多少？（230-50）。

其实这道题相对来说还比较简单，如果换一个问题，比如：一只东北虎和一只大熊猫的体积共有多少千克？那就可能真会难道相当部分孩子的。不管怎么样，解题思路仍然应该以画线段图的方式来帮助理解，我觉得这是每个孩子必须学到的一种基本技能：

以上是我个人的理解，也许过于复杂，或者有更好的思路和方法来解决这个问题，特别是对于中差生来说，真的让他们能够理解并完整的做对这道题确实是为难他们了，更难以要求他们能够掌握这样的思路。

甲数是230,比乙数的2倍还多50,乙数是多少？

这是一道整数应用题，涉及到两个量，甲数和乙数，甲数是230，且知道乙数与甲数的关系，求乙数。这里面涉及标准量和比较量，有点类似高年级要学习分数应用题时候去寻找单位1的量，一般来说,标准量通常在“比”“占”“是”的关键字的后面，在列式中，这些表示关系的式子经常用“=”来替代。

做应用题关键在在理清题目的含义，找到关系式，这个题目的关系式是什么呢？

甲数和乙数之间的关系，乙数是标准量，甲数是比较量，甲数比乙数的2倍还多50，如何理解呢？甲数比乙数多，多多少呢？2倍还多50,。

通过这句话可以得到甲数与乙数之间的关系式字，这是本题目的关键，

甲数=乙数×2+50.

在读题和理解题目的含义中需要做到文字语言的转化，在这个题目中写关系式的时候，把“比”直接用“＝”给替代。

写出关系式子后剩下的就比较好处理了。

有了等量关系式，可以用方程的方法来解答。

解方程即可求出乙数，比较简单。

对于低年级的孩子来说，方程还没有学习，那么该如何来解答这道题目呢？

首先还是得分析题意找出题目中的关系：

甲数=乙数×2+50，这是本题的核心。

在低年级的时候，学生已经学习了用线段图来表示具体的数量，结合题意，可以画出线段关系图来，画线段图的关键还是首先来确定标准量和比较量以及它们之间的关系

用一份来表示乙数，再根据甲数等于乙数的2倍还多50 ，则甲数可以用两份来表示，再用一段来表示多出的50即可。

线段图如下：

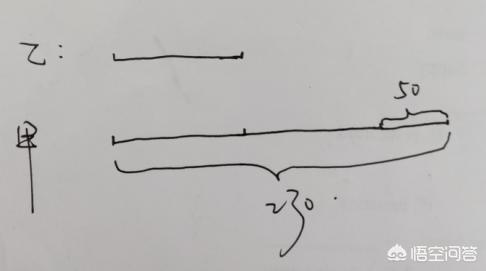
线段图画出之后题目就很容易理解和解答了，

可以直接列出算式（230-50）÷2,计算可以直接求出一份的数量，也就是乙数的大小。

对于低年级的学生，比较建议用画线段的方法来解答这样的题目，线段图分析起来比较直观和形象，比较容易找到思路和方法，是数形结合思想的雏形，在解决很多的题目中都会运用，是小学学生必须要掌握的解题思路和方法。

2X+50=230

2X=230-50

2X=180

X=180÷2

X=90（乙数为90）

感谢邀请！先上答案：乙数为90。这是一道入门级的低年级课外培优倍数关系应用题，常见于二，三年级课外培优。我是王老师，专注于小学数学，很高兴为您答疑解惑！分享解题策略，推广趣味数学，提供家庭辅导建议，欢迎您的关注！7~8岁年龄段处于具象思维阶段，从二年级的两步混合运算应用题开始，应用题逐步以文字叙述题目出现，这对于差生来讲，面对抽象的文字，隐藏的数量关系，确实有一定的挑战。如何让孩子理解解题步骤，并逐步转化为自己面对问题的思考方式呢，以下详解，供您参考！

基础倍数关系应用题~图示建模+转化思想

王老师向来反对过早使用方程思想，一方面孩子还缺少必要的知识准备，另外也限制数学思维综合发展。回到题目，摘抄如下。

甲数是230,比乙数的2倍还多50,乙数是多少？如何用更容易理解的方法讲给差生？

以下为王老师的图示建模思考引导方法：

① 读懂题目

题目中涉及几个数量？甲数和乙数

两个数量哪个大一些？甲数

问题问得是什么？乙数是多少？

首先确定语言理解是否有问题，一些阅读理解比较弱的学生，要适当帮助它们改动题目的陈述方式，使得题目内在的各种关系变得明朗一些。

② 改写题目

数学题的标准陈述往往比较标准、简练，到孩子自己表达改写，实际上是对于文字结构的理解。这也是通过更新语义从而解构的过程，关键是对于数字和关键词选择。

甲数比乙数的2倍还多50，知道甲数是230。

③ 建立分析模型~方块图图示建模

抽象的文字下面藏着数量关系，如何让孩子直观进行观察呢，这就是需要用到方块图来表示数量，将数学问题可视化。

→ 乙数比较小，我们把它看成“1份量”，用一个方块图来表示。

通过引导学生用图示建立模型，这样就可以直观看到乙数这个数量了。

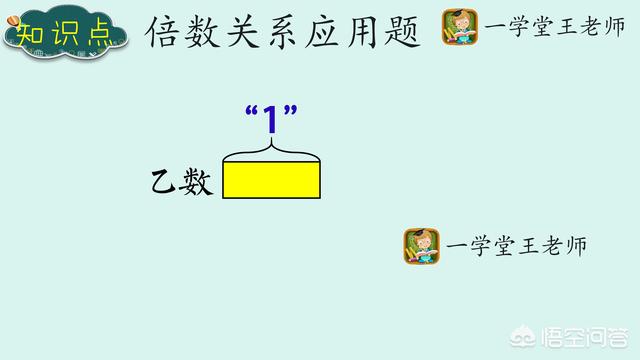
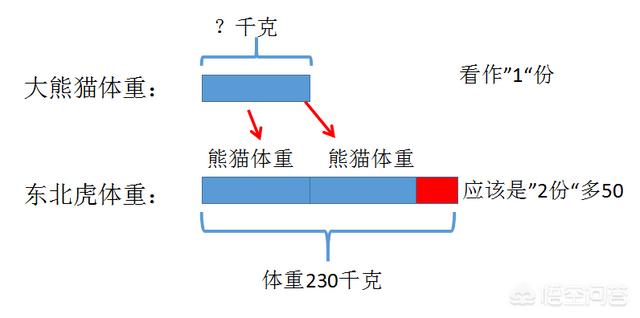
→ 甲数该怎么画呢？

回到孩子自己理解表述，甲数比乙数的2倍还多50，那就首先要画出两个同样的方块，这样够吗？不够，还需要再加上一个表示50的方块。如下图示：

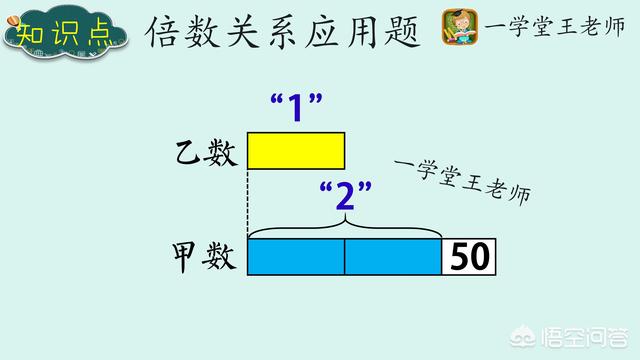
题目中还知道什么信息呢？引导学生说出甲数等于230，这样我们就把方块图画好了。

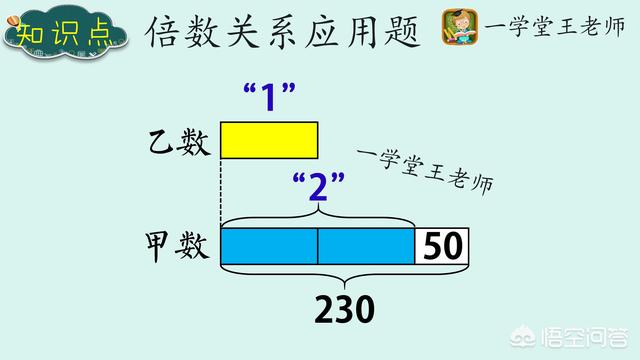
④ 对数量关系进行直观观察分析

画出图来，相当于把抽象的文字转化成形象的图标，让孩子通过对于具象的观察，找出数量之间的关系。观察甲数，你能发现什么？

这时就要引导孩子进行转化，甲数去掉50部分，就变成了乙数的整数倍

→ 2份量：230-50=180

→ 1份量(乙数)：180÷2=90

通过观察多份量，目标是求出一份量等于多少。

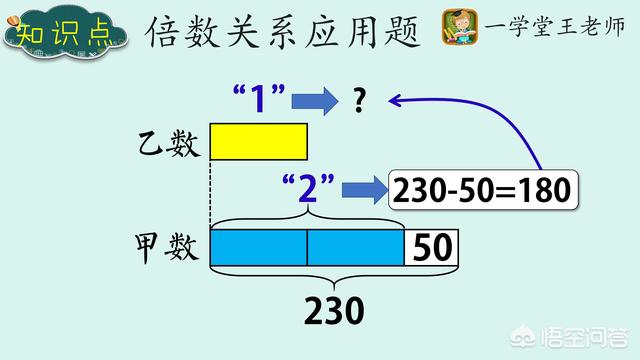
⑤ 列出综合算式并计算，作答

→ (230-50)÷2=90，乙数为90。通过图示，就可以引导孩子说出每一步运算的含义了。答略

⑥ 验算

把计算结果带入到题目中，看看是否符合题目要求。90×2+50=230。

让学生养成验算的好习惯。

结语

这就是王老师的引导过程，通过画图建模，可以让孩子有思考工具，从而将抽象问题具象化，便于理解和沟通已知与未知的联系，比死记硬背数量关系公式更有效果！系统学习各类应用题的图示建模方法，欢迎关注王老师数学专栏。

欢迎关注王老师头条号及尚可网

学习更多好玩有趣的数学学习方法

线段法很容易，一般都能懂

要真了解学生，差到哪种程度。按一般思维，我们所知道的差生，可以换一种说法，并且，把长句子变成短句子加以引导。例如，230如果减去50，还剩多少？这个问题学生应该能解决的。然后在化解。这个数，跟乙什么关系呢？正好是乙的几倍！

当然，如果孩子智力停留在过去某个阶段，可以转化为另一个题。让学生说出自己的年龄，然后老师说自己的年龄是学生的二倍，猜一猜老师今年多大？这种问题学生还比较喜欢，且踊跃思考，积极回答。

曾经我听过有人说，没有学不会的学生，只有不会教的老师。当年很生气，曾经想过，这个人一定没教过差生。后来慢慢发现，只要孩子不是智障问题，老师只要不停地去创新教学方法，一定会把孩子都教好的！

对于学困生或者低龄段学生来说，图像法无疑是最直观最简单的方法了，这也是数形结合思想的初步应用，对于今后学习数形结合来说有一定的作用！数形结合思想在今后的数学学习中很多地方都会都会运用，也是数学学习中非常重要的思想方法，所以最好从小学开始就理解这种解题思路和方法。

对于这道题目来说，画出线段图对学生理解来说更加直观和形象，也最容易找到思路和方法。

分析题意画出线段图

题目中说甲数是230，比乙数的2倍多50，那么我们就可以把乙数看成“1”(图中线段EF)，则甲数的图像就可以看成线段AD，其中AC＝2AB=2EF。那么乙数就等于甲数减去50除于2，也就等于90.

本题答案就为:90

解题过程:

解:(230-50)÷2＝90

答:乙数为90

注意:从小一定要养成检查的习惯，根据题意我们可知90×2＋50＝230.说明答案成立。

列方程解应用题

对于高年级学生来说，只要设未知数建立简单的一元一次方便即可。

具体过程:

解设乙数为x

则2x＋50＝230

解得x＝90

答:乙数为90

反思:学习数学一定要注意引导孩子形成数学思维，而不是成为刷题的工具，要教会孩子分析问题的思路，对于此题建议在讲解时让孩子自己去画图，可以多提醒但是别告知，直到ta能画出图像理解题意为止。

1.看他的困惑点在哪里。有的学生对甲乙丙丁之类的表述，一见到就晕，对这一类，你可以试着替换成老师有230块钱，比学生多很多，多多少呢？是学生的2倍还要多50块。这样，他好理解一些。

2.有的题目表述难看懂。比乙数的2倍多50这句话，需要分开来帮他理顺：先是甲比乙多，多太多了，哪怕2个乙都没有甲一样多，还要加50才能和甲一样。

这道题简单，问几个问题就可以了。

一、甲数怎样才能是乙数的2倍？（答:甲数去掉50就是乙数的2倍。列式为230-50）

二、（230-50）是乙数的2倍，怎样才能和乙数同样多？（答:要把（230-50）平均分成2份。列式为（230-50）/2）

你看，问题解决了。

解题思路就是把复杂的问题按逻辑关系分解成简单的问题就容易多了。

设乙数为X ，所以2X＋50＝230， X二90 。即甲数为230而乙数为90。

用这个例子：把甲数看作8，甲数是乙数的2倍多2，可求得乙数为3。如果还不理解就是二年级的水平了。

我来讲的话，就是让学生理解题意。第一，甲数是乙数的2倍吗？怎么才是乙数的2倍？明确第一步用减法！第二，知道乙数的2倍是多少，求乙数？这样就好做了！

我是230，比你的两倍还多50，或者我有230，是你有的两倍还多50。

那位说还是看不明白解答的同学，我给你一个更简单的方法。

一、解题

我先问你一下，如果这道题换一个方式出题，改成这样：甲是230，比乙多50，乙数是多少？

那么你会吗？你肯定会，你的答案是：乙是230-50=180。

很好。现在把“乙”替换成“乙的二倍”，也就是说“乙的二倍”是230-50=180，那么现在的乙是多少。我想这个时候你肯定也会，既然“乙的二倍”是180，那么乙就是180÷2=90。

你会发现，如果把“乙的二倍”看成一个整体，那么这道题，就变成了一年级的简单算术题。就类似于这样一道题：小明的爸爸身高230厘米，比小明高50厘米，小明身高是他弟弟小亮身高的2倍，请问弟弟小亮身高是多少？

如果你还是觉得有点糊涂，让我们再回到原题。如果一道题很容易理解，那么它一定是比较简单的题，因为数学知识是一环扣一环的。那么怎么样把它变得非常简单呢？

把“乙数的二倍”简称“乙二”，你甚至可以直接把他看成一个人名儿，类似于张三李四王五。那么原题就变成了：

甲数是230，比“乙二”多50，乙数是多少？

首先列出求“乙二”的算式，230-50=180，然后把“乙二”÷2得90。完整的算式是（230-50）÷2=90。

所以这道题的解题关键是，把“什么什么的多少倍”看成一个整体，同时搞清楚到底是：谁比谁多，谁比谁少。

二、差生该怎么学会解类似的题？

题主老师说学生错误的原因多数是，只看到了数字和关键词，例如“倍数”用乘法，“多”就用加法等。没错，这是大部分数学学习困难的学生会用的方法。这种方法在认知心理学中叫做直接转换策略，是最低效且容易出错的策略。

有的老师用线段图来解释，这是非常好的。这种策略叫做结构策略，或者画图策略。这种策略非常高效，从二年级就能用得上，到初中学几何的时候，就更是如虎添翼。但是对于数学实在差的学生来说，还需要一个训练过程。不过这位同学你也不要担心，这个训练过程不会很长。

我刚才介绍的这种策略叫做问题模式策略。就这道题来说，这种策略就是把学生觉得复杂难懂的题型模式，转换成他已经学会的很熟悉的题型模式。 （仅仅是就这道题来说，实际上还要再复杂一些）

能把一个乘除混合运算，转换成相对简单的加减运算，是这种策略的一个优势，很适合学习困难的学生。不过这并不是说，学习好的学生不会用这种策略。相反的是，学习好的学生，很早就学会了这种策略。

三、出错的根本原因是：出题顺序和学生喜欢的不一样

我们还可以深挖一下，这样的题学生出错的根本原因。如果把这道题改变一下，我想大多数的学生都会做。甲数是230，乙数的2倍比它少50，乙数是多少？

这道题的难度显然比原题要小一些，因为这是学生习惯的顺序。通俗一点说，就是这道题是顺着来的。先给出一个量，第2个量跟它有什么关系，那么第2个量是多少？学生比较喜欢这样的顺序。

所以做这样的题，很重要的一个步骤就是把顺序重新理正。理正的时候，就涉及到我讲题的时候说的，把“什么什么的多少倍”这种信息，看成一个整体。

所以总结一下，就是一看成整体，二理正顺序。

说的甲比一个数多5O，而这个数的一半是乙。这样说应能听得懂了吧。

小孩子一定要早点开始练习画图。很多孩子不画图对着空气发呆，一画图，就明白了。

很简单的！既然230比乙数的2倍还多50，那么230-50＝180则这180是乙数的2倍，乙数就是90啊！

甲数比乙数的2倍还多50，那么甲数减掉50就跟乙数的2倍一样多了。甲数是230，减掉50就是230-50＝180，即180是乙数的两倍。那么乙数就是180的一半，即乙数＝180÷2＝90。

不好意思，各位老师，我就是那位差生，你们的方法我还是看不会！[笑哭]

这个题都会做，但是你要用最简单易等的方法，让学听等，应当采用画线段的方法，因为以后有很多解方程的应用题都能用到，这对以后的学习，很有好处，这就是打基础。